اطلاعیه

کنفرانس فیزیک ایران

دانشگاه فردوسی مشهد

2 تا 5 شهریور ماه سال 1394

زاویه حد

زاویه حد(Critical Angle)
 

تعریف:

اگر تابش از محیط غلیظ با ضریب شکست بالا بر محیط رقیق با ضریب شکست پایین صورت گیرد (n1>n2) بنابراین قانون اسنل با این شرایط ، مبهم می شود. زیرا
(sin r=n1/n2 sin i) که در آن(1< n2/1n) بنابر این احتمال دارد، برای i های بزرگ sin r بزرگتر از واحد شود. پس یک زاویه بحرانی تعریف می کنیم که حد بیشینه sin r را به ما دهد که برابر واحد یا زاویه اش r=90 هست.

یعنی به ازای sin r=1 خواهیم داشت زاویه حد (c=i) را که از رابطه زیر یافت می شود: (c=arcsin n2/n1)
به عنوان مثال اگر تابش از هوا بر شیشه باشد داریم:n=1.5 بنابراین درجه c~41 خواهد شد. بهتر است بدانید کهc از کلمه لاتین Critical به معنی بحرانی اخذ شده است.
 

 

مفهوم فیزیکی:

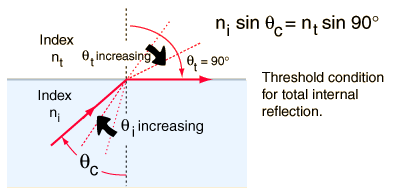زاویه شکست نود درجه (90) بدان معنی است که پرتوی عبوری از مسیری قائم بر خط عمود (موازی فصل مشترک دو محیط)خواهد داشت به عبارتی در زوایای بزرگتر از C ، عبوری بر محیط دوم نخواهیم داشت.

آینه های دی الکتریک(آینه های چند لایه ای)

دید کلی:

بسیاری از مواد فلزی مانند آلومینیوم(Al)، نقره(Ag)و طلا(Au) در مقایسه با سایر مواد ، باز تابنده هستند، امّا آنها نیز بخشی از تابش فرودی را جذب می کنند. دربرخی کاربرد ها، خاصه در آنهایی که شامل لیزرهای پر توان هستنداین جذب حتی اگر "اندک" باشد تابش دارای انرژی کافی برای تبخیر مواد است و آنها را به عنوان یک آینه از کار می اندازد و خاصیت آینه ای را از آنها سلب می کندو آینه را خراب می کند.
در این کاربردها و موارد مشابه آن، طراح اپتیکی باید از آینه هایی استفاده کند که مطلقا از مواد دی الکتریک که تابش واقعا ناچیزی در ناحیه مورد نظر جذب می کنند، یا به طورکلی جذب نمی کنند، ساخته شده باشند این آینه های دی الکتریک از لایه های متناوب موادی با ضریب شکست بالا و پایین تشکیل می یابند هر لایه دارای ضخامتی برابر با یک چهارم یا نصف طول موج نوری که به آینه می تابد، می باشد این روش در پوشش های دی الکتریک به راحتی قابل اعمال است.(به این روش در اصطلاح علمی روش لایه نشانی گویند)
اپتیکی حاکم بر آینه ها ی دی الکتریک و نحوه عملشان:'>

قوانین اپتیکی حاکم بر آینه های دی الکتریک و نحوه عملشان:

جبهه موج

 

 

 

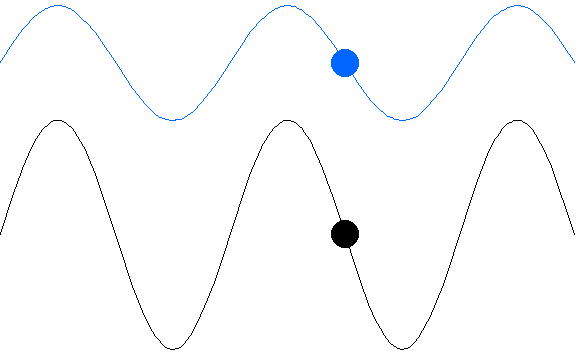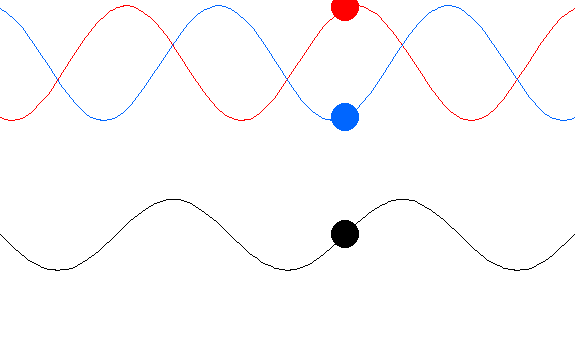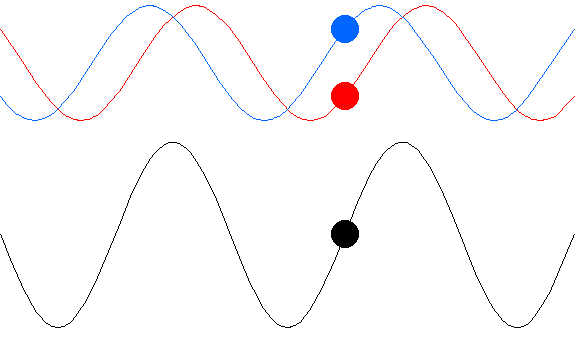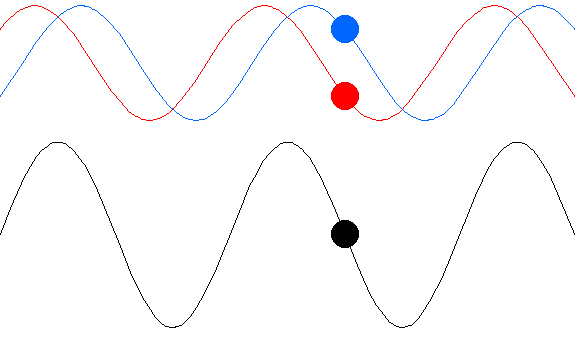
مفهوم جبهه موج بیان مناسبی برای انتشار هر نوع موج است. بنا بر تعریف ، مکان هندسی نقاطی که فاز ارتعاش یک کمیت فیزیکی متعلق به موج در آنها یکسان باشند، جبهه موج نامیده می‌‌شوند.

مقدمه

اگر یک ریسمان را از دو انتها به یک نقطه ثابت متصل کنیم، سپس یک تکه از ریسمان گرفته و اندکی کشیده و رها کنیم، در طول ریسمان یک تپ ایجاد می‌‌شود که در طول آن حرکت می‌‌کند. این آشفتگی یا تپ نمونه‌ای از یک حرکت موجی است. در حالت کلی ، یک تپ سه بعدی را در نظر بگیرید. می‌‌توان سطوحی را رسم کرد که از تمام نقاطی که در یک لحظه معین دارای آشفتگی مشابه هستند، بگذرد. با گذشت زمان این سطح نیز حرکت می‌‌کند و نشان می‌‌دهد که تپ چگونه منتشر می‌‌شود. برای تپهای بعدی نیز می‌‌توان سطوح مشابهی رسم کرد.

ترسیم پرتو

توصیف کلی

یکی از سودمندترین روشها در طراحی اپتیکی ، مطالعه سریع اجزای سیستم آنها و مسیر نور در آنها است. این کار همانند طراحی سریعی است که یک نقاش قبل از تصمیم گیری نهایی روی ترکیب رنگها انجام می‌دهد. ابتدائی‌ترین شکل آن ، طرح مقدماتی با یک عدسی شیئی غالبا نامشخص شروع می‌شود. سپس یک سری از عدسیها ، آینه‌ها ، منشورها ، مدوله کننده‌ها ، آشکارسازهای نوری و اجزای دیگر اپتیکی بصورت متوالی و پشت سر هم قرارداده می‌شوند. و همراه آن چند پرتو مهم عبوری از این اجزا ، در طول مسیرهایی که از طریق محاسبات مسیر پرتو تخمین زده شده‌اند، ترسیم می‌شوند.

انسان،‌ امواج مادون قرمز را می‌بیند!

بیگ بنگ: براساس تحقیقات جدید منتشر شده در سری مقالات آکادمی ملی علوم، دانشمندان معتقدند انسان درجه‌ای از دید مادون قرمز دارد و ممکن است تا حدی قادر به دیدن اشعه مادون قرمز به‌عنوان نور قابل مشاهده باشد.

ه گزارش بیگ بنگ به نقل از جام جم، تحقیقات قبلی اشاره کرده بود انسان نمی تواند کاملا به بخش قابل رویت طیف مادون قرمز محدود باشد. اما این تحقیقات به این که دیدن محدوده ای از امواج مادون قرمز امکان پذیر است هیچ اشاره ای نداشت. دانشمندان به رهبری کرزیستوف پالزوفسکی در دانشگاه کیس وسترن رزرو کلیولند هنگامی که مشغول انجام آزمایش های دیگری بودند، متوجه شدند قادر به دیدن پرتو های لیزری مادون قرمز با نور سبز کم رنگ هستند. در نتیجه تشویق شدند تا در پی کسب اطلاعات بیشتری درباره توانایی دیدن طیف مادون قرمز توسط چشم انسان باشند.

آنها شروع به آزمایش همان پالس ها روی ۳۰ نفر داوطلب کردند. همه آنها قادر به دیدن پالس های لیزری نزدیک به مادون قرمز به عنوان نور مرئی بودند. آنها پالس های کوتاه را به رنگ سبز و پالس های بلند را به رنگ قرمز می دیدند. پالزوفسکی می گوید: این کشف باعث شده تا بتوانیم بگوییم باید دامنه دید انسان را گسترده تر در نظر بگیریم. بینایی انسان به فوتون های نور بستگی دارد که سلول های گیرنده نور را در شبکیه چشم تحریک می کنند. معمولا رنگدانه های حساس به نور در گیرنده های نوری شبکیه فقط با طول موج های مرئی نور فعال می شوند.

با این حال دانشمندان دریافته اند این رنگدانه ها در صورت دریافت دو فوتون همزمان طیف مادون قرمز می تواند طول موج مادون قرمز بلندتر نور را ببیند. پالزوفسکی می گوید: دو فوتون طیف مادون قرمز با طول موج بلند تر همان کاری را می کنند که یک فوتون با طول موج مرئی و کوتاه تر انجام می دهد. پالزوفسکی می گوید: این تحقیق نشان می دهد که متخصصان چشم می تواند از پرتوهای لیزر مادون قرمز برای اسکن شبکیه و تشخیص مشکلات چشمی در مراحل اولیه بیماری و قبل از تبدیل شدن به یک مشکل درمان نشدنی استفاده کنند. در حالی که در این شرایط ممکن است استفاده از لیزر با طول موج مرئی به شبکیه آسیب رساند.

سایت علمی بیگ بنگ / منبع: popularmechanics / مترجم: آتنا حسن آبادی

لیزر الکترون آزاد

لیزرها اکثراً براساس مفهوم وارون سازی جمععیت بین ترازهای انرژی حالت‌های مقید جدا از هم مواد بوده‌اند یعنی الکترون‌ها یا به اتم و ملکول متصل بوده‌اند ویا الکترون‌ها در طول چندین اتم در حرکت بوده‌اند.( مثل لیزر dye) ویا الکترون قادر است که در تمام بلور ازادنه حرکت کند( مثل لیزرهای نیم رسانا). حالا یکی از جالب ترین و جدیدترین لیزرها را توضیح می‌دهیم که الکترون‌ها نسبت به این موارد مذکور ازادی حرکت شان باز هم بیشتر است. اساس لیزر الکترون ازاد نوسان الکترون در یک خلاء که از هر محیط بهره مادی تهی است. اساس لیزر باریکه الکترونی با سرعت نزدیک به سرعت نور از میدان مغناطیسی متناوبی که به ان جنباننده می گویند عبور می‌کند. سرعت نسبیتی الکترون‌ها , برای انتقال از بسامد پایینی که دستکاه مختصات سوار بر الکترون مشاهده می‌شود، باعث نوسان بسامدی می‌شود.

بسامد تابش توسط انرژی جنبشی الکترون‌ها و همچنین دوره ساختار میدان مغناطیسی تناوبی تعیین می‌شود. اینه‌های لیزری در دو انتهای مخالف ساختار مغناطیسی و عمود بر جهت الکترون‌ها به منظور ارسال یک بخش از انرژی تشعشع شده به عقب این ساختار مغناطیسی قرار داده می‌شود، بنابراین یک الگوی تشعشعی از موج ایستاده بین اینه‌ها ایجاد می‌گردد. فرایند القایی ، از بر همنکنش لیزر الکترون‌های نسبیتی (که از ساختار مغناطیسی عبور می‌کنند) بدست می اید. . توصیف دقیق لیزر الکترون آزاد نیازمند بکارگیری نظریه نسبیت است،ولی بعضی مفاهیم اصلی را بدون آن نیز می توان درک کرد. می دانیم که الکترون شتابدار تابش می‌کند و نیز با تابش ناشی از یک انتن که در آن بارها در طول مسیری ثابت به جلو و عقب نوسان می‌کنند آشنا هستیم.

کوانتیزه کردن

در فیزیک کوانتیزه‌کردن (به انگلیسی: quantization) روند گذار از درک کلاسیک از پدیده‌های فیزیکی به درک جدیدتر شناخته شده به عنوان مکانیک کوانتوم است. این روش برای ساختار نظریه میدان‌های کوانتومی بر مبنای تئوری میدان (فیزیک) است. در کل این روش برای ساخت مکانیک کوانتوم بر مبنای مکانیک کلاسیک بود. کوانتیزه‌کردن میدانی فرایند کوانتیزه‌کردن میدان الکترومغناطیسی است که در این فرایند فوتون‌ها کوانتم میدانی هستند. این فرایند مبنای تئوری‌هایی چون فیزیک ذرات، فیزیک هسته‌ای، فیزیک ماده چگال و نورشناخت کوانتومی است. کوانتیزه‌کردن میدان کلاسیک را به حالت کوانتومی تبدیل می‌کند که در آن حالت خلاء کم ترین حالت انرژی است. از بارز ترین نیازها برای انجام روند کوانتیزه‌کردن استفاده از بازبه‌هنجارسازی است. یکی از نخستین روش‌ها که برای کوانتیزه‌کردن استفاده گشت، کوانتیزه‌کردن کانونیک بود گرچه روش‌های دیگری وجود دارند که در بیشتر شرایط برای محاسبهٔ دامنه‌های کوانتومی بیشتری مورد استفاده واقع می‌شوند.

کوانتیزه‌کردن کانونیک

کوانتیزه کردن کانونیک (به انگلیسی: Canonical quantization) در فیزیک یک رویه برای اندازه‌گیری یک نظریه کلاسیک است که سهمی در ساختار رسمی، مانند تناسب نظریه کلاسیک دارد. به طور تاریخی کوانتیزیشن کانونیک روش هایزنبرگ برای بدست آوردن مکانیک کوانتم نبودبلکه دیراک آن را در تز دکترای خود در سال۱۹۲۶ با عنوان روش کلاسیک برای کوانتیزه کردن معرفی کرد وبه شرح آن در متن کلاسیک خود پرداخت. کلمه کانونیک از نزدیک بودن هامیلتونی به مکانیک کلاسیک به وجود آمده که در آن حرکت‌های سیستم به وسیلهٔ براکت‌های پواسون کانونیک، ساختاری که فقط در کوانتیزه کردن کانونیک حفظ می‌شود، ایجاد می‌گردد. این روش توسط دیراک در ساختار الکترو دینامیک کوانتمی بیشتر به معنی نظریه میدان کوانتمی استفاده می‌شد. در نظریه میدان، این روش همچنین کوانتیزه ثانویه نامیده می‌شودکه در مقابل کوانتیزه اولیه نیمه کلاسیک برای ذرات واحد است.

دیگر روش‌های کوانتیزه کردن

• کوانتیزه کردن ویگنر-وایل (به انگلیسی: Wigner–Weyl transform)
• کوانتیزه کردن هندسی (به انگلیسی: Geometric quantization) که با استفاده از ریاضیات و بر مبنای درک کلاسیک انجام می‌شود.
• کوانتیزه کردن حلقه‌ای (به انگلیسی: Loop quantization)
• کوانتیزه کردن دگرشکلی (به انگلیسی: Deformation quantization)
• کوانتیزه کردن جدایی ناپذیر (به انگلیسی: Path integral quantization)
• کوانتیزه کردن مکانیک آماری کوانتومی (به انگلیسی: Quantum statistical mechanics approach)
• کوانتیزه کردن مکانیک تغییری شوازینگر (به انگلیسی: Schwinger's variational approa  )

کروشه پواسون

در ریاضیات و مکانیک کلاسیک کروشهٔ پواسون (Poisson bracket) عمل‌گری عمده در مکانیک هامیلتونی است. کروشه پواسون همچنین ارتباط مستقیمی بین مکانیک کوانتم و مکانیک کلاسیک برقرار می کنند.

مختصات استاندارد

در مختصات ذاتی برروی فضای فاز، اجراء عمل دوتایی کروشهٔ پواسون، در مورد دو تابع مفروض 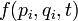و در فضای فاز و زمان، فرم زیر را به‌خود می‌گیرد:

معادلات حرکت هامیلتون

معادلات ژاکوبی-هامیلتون را می‌توان بر حسب کروشهٔ پواسون به‌صورت معادل زیر هم بیان کرد. این موضوع را می‌شود به طور مستقیم در یک دستگاه مختصات عادی نشان داد. فرض می‌کنید تابعی است بر روی یک خمینه. آنگاه داریم:

 

پدیدة کامپتون

پدیدة کامپتون

 

نویسنده: محمدرضا عظیمی


 

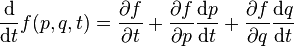
یکی از بهترین آزمایشاتی که به وسیله آن می توان خاصیت ذره ای نور را مشاهده کرد و دریافت، اثر کامپتون است. این پدیده را که نمی توان آنرا در پرتو فیزیک کلاسیک توجیه کرد آرتور هالی کامپتون در سال 1922 کشف کرده است. وی طی آزمایشی نشان داد که با تابیدن نور با بسامد (رنگ) مشخص بر سطح فلزی براق، الکترون ها و فوتون ها به صورت ذره ای با یکدیگر برخورد می کنند.
با ابعادی ریزتر به این اثر نگاه می کنیم: در هنگام تابش یک فوتون ب